
排序算法(Sorting algorithm)是一类很基础的算法。其研究的问题是:给定 $N$ 个数 ${a_{1},a_{2},\dots,a_{N}}$,使其按照一定的顺序排列。本文通过排序方法和计算复杂度就经常会遇到的六种排序算法作以介绍。
排序算法的分类
按照不同的分类指标,可以有很多种排序算法的分类。具体的:
稳定性
在给定的 $N$ 个数 ${a_{1},a_{2},\dots,a_{N}}$ 中,如果 $a_{j}=a_{k}, j \lt k$。稳定的算法在排序结束后,$a_{j}$ 依然排在 $a_{k}$ 的前面。即稳定的算法不改变相同数据的前后位置。根据算法的稳定性,算法分为稳定的算法和不稳定的算法。
计算复杂度
计算复杂度衡量算法随着输入数据规模 $N$ 的增加所需要的时间和空间的变化。把每次元操作(比较、移动、换位)所耗费的时间看作单位时间 $T_{c}$,每个数据占用的空间看作单位空间。根据输入数据的不确定性,算法有最好情况(已经是有序状态)复杂度、最差情况(完全无序)复杂度和平均复杂度。不同的排序算法有着不同的计算复杂度,一般来说我们不可能同时减少时间复杂度和空间复杂度。
是否进行了比较
有的排序算法运行过程中会在数据之间进行比较,有的则不会。
排序算法介绍
冒泡排序
冒泡排序把数据看作一些大小不一的「泡泡」,两个泡泡相遇,大的「泡泡」会向上(右)飘,小的「泡泡」会向下(左)沉。在排序时,从最左边的「泡泡」开始,它和右边相邻的「泡泡」有一次相遇,大的「泡泡」向右,小的「泡泡」向左。一次扫描过后,最大的「泡泡」会漂浮在顶端,完成它的排序。最多经历 $N$ 次扫描,算法完成排序。
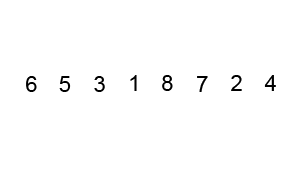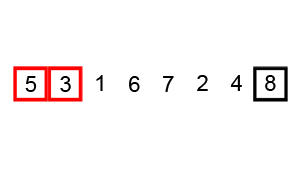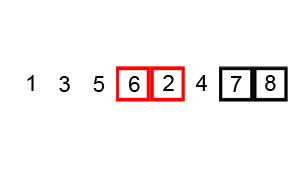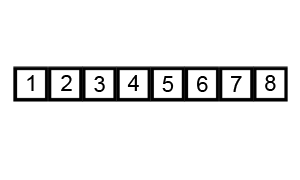
复杂度分析
在冒泡排序中,算法每次进行扫描都需要进行比较。第 $n$ 次扫描,产生 $N-n$ 次比较。完成排序共产生 $\sum_{n = 1}^{N} (N-n) \approx \frac{n^{2}}{2}$ 次比较。
算法在最坏的情况下,即每次比较都需要换位置。第 $n$ 次扫描,产生 $N-n$ 次换位。完成排序共产生 $\sum_{n = 1}^{N} (N-n) \approx \frac{n^{2}}{2}$ 次换位。在最好的情况下,不需要换位。
故冒泡排序算法的时间复杂度为 $O(n^{2})$。
选择排序
选择排序就是重复「从待排序的数据中寻找最小值,将其与序列最左边的数字进行交换」这一操作的算法。在序列中寻找最小值时使用的是线性查找。
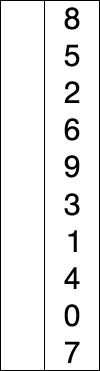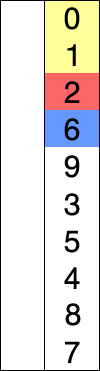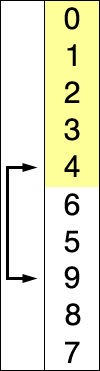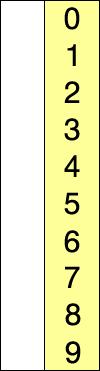
复杂度分析
选择排序使用了线性查找来寻找最小值,其每次扫描过程中的比较操作和冒泡排序一样,共有 $\sum_{n = 1}^{N} (N-n) \approx \frac{n^{2}}{2}$ 次比较。
每轮中交换数字的次数最多为 1 次。如果输入数据就是按从小到大的顺序排列的,便不需要进行任何交换。选择排序的时间复杂度也和冒泡排序的一样,都为 $O(n^{2})$。
插入排序
插入排序是一种从序列左端开始依次对数据进行排序的算法。在排序过程中,左侧的数据陆续归位,而右侧留下的就是还未被排序的数据。插入排序的思路就是从右侧的未排序区域内取出一个数据,然后将它插入到已排序区域内合适的位置上。
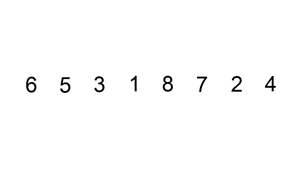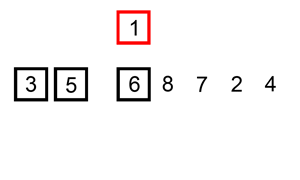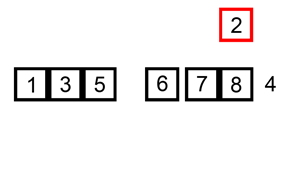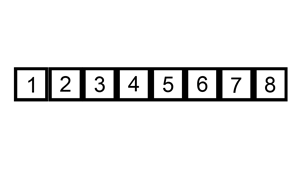
复杂度分析
在最坏的情况下,即数据完全倒序。对第 $n$ 个数据进行插入排序,每次在插入的时候都需要比较$n-1$次,所以时间复杂度和冒泡排序的一样,都为 $O(n^{2})$。
堆排序
堆排序依赖于数据结构堆。堆可以理解为一棵树,其父结点的值要大于子节点的值。这样在堆建完之后,从降序排列的堆中取出数据时会从最大的数据开始取,所以将取出的数据反序输出,排序就完成了。

复杂度分析
堆排序一开始需要将$n$个数据存储到堆里,所需时间为 $O(n \log_{2} n)$,在排序的过程中,堆从空堆的状态开始,逐渐被填满。由于堆的高度小于 $\log_{2} n$,因此插入数据所需时间为 $n \log_{2} n$。排序是一个取数据的过程,取完数据还需要重建堆。取出数据再重建堆的时间为 $\log_{2} n$,共有 $n$ 个数据,因此排序的过程耗时 $n \log_{2} n$,总的时间复杂度为 $O(n \log_{2} n)$。
归并排序
归并排序利用了分而治之的思想。具体的,归并排序算法会把序列分成长度相同的两个子序列,当无法继续往下分时(也就是每个子序列中只有一个数据时),就对子序列进行归并。归并指的是把两个排好序的子序列合并成一个有序序列。该操作会一直重复执行,直到所有子序列都归并为一个整体为止。
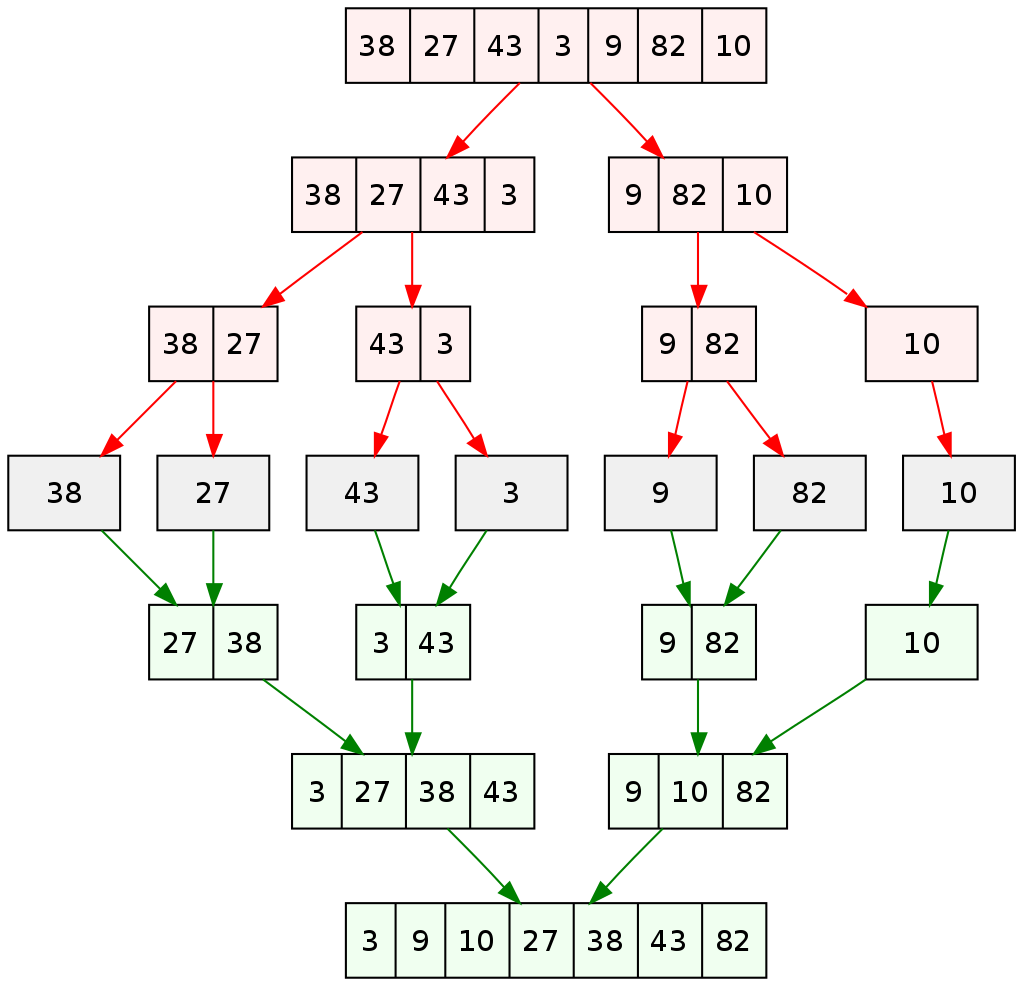
复杂度分析
归并排序中,分割序列所花费的时间可以不计,因为我们可以当作序列本来就是分割好的。在合并子序列的时候,需要比较首位数据的大小,然后移动较小的数据,因此只需要花费和两个子序列长度相同的运行时间。故完成一行归并花费的时间就是 $n$,共有 $\log_{2} n$ 行,因此归并排序的时间复杂度为 $n \log_{2} n$。
快速排序
快速排序首先选择一个基准数据,一轮排序后,大于基准数据的数据全部在基准数据的右边,小于基准数据的数据全部在基准数据的左边。这样基准数据在一轮排序中就找到了自己的位置,对于左边和右边的数据,一直按照快速排序排列下去,直到排序完毕。
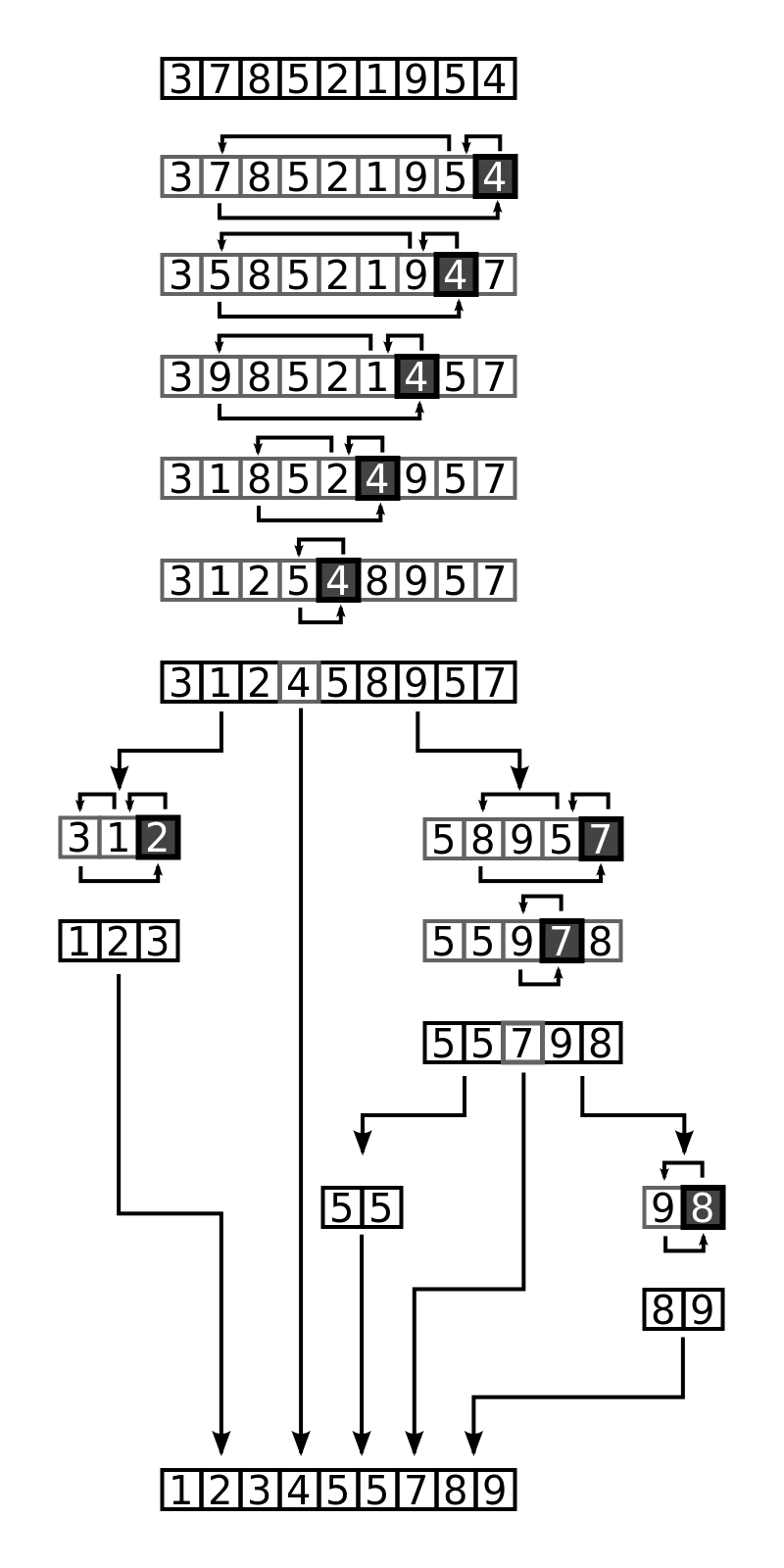
复杂度分析
快速排序也利用了分而治之的思想,它将原本的问题分成两个子问题(比基准值小的数和比基准值大的数),然后再分别解决这两个问题。
分割子序列时需要选择基准值,如果每次选择的基准值都能使得两个子序列的长度为原本的一半,那么快速排序的运行时间和归并排序的一样,都为 $n \log_{2} n$。如果运气不好,每次都选择最小值作为基准值,那么每次都需要把其他数据移到基准值的右边,递归执行 $n$ 行,运行时间也就成了 $O(n^{2})$。
排序算法比较
上述介绍的6种排序算法中,其时间复杂度和空间复杂度都有所不同,下面的表格给出了这6种排序算法之间的比较。
| 名称 | 最好情况下 | 平均情况下 | 最差情况下 | 存储占用 | 是否稳定 |
|---|---|---|---|---|---|
| 冒泡排序 | $O(n)$ | $O(n^{2})$ | $O(n^{2})$ | $ 1 $ | 是 |
| 选择排序 | $O(n^{2})$ | $O(n^{2})$ | $O(n^{2})$ | $1$ | 不是 |
| 插入排序 | $O(n)$ | $O(n^{2})$ | $O(n^{2})$ | $1 $ | 是 |
| 堆排序 | $n \log_{2} n$ | $n \log_{2} n$ | $n \log_{2} n$ | $1$ | 不是 |
| 归并排序 | $n \log_{2} n$ | $n \log_{2} n$ | $n \log_{2} n$ | $n$ | 是 |
| 快速排序 | $n \log_{2} n$ | $n \log_{2} n$ | $n^{2}$ | $\log_{2} n $ | 是 |
—全文完—